보충자료1. Normal Mode

Normal mode는 모든 원자들이 공통의 주기 T 로 같은 운동을 반복하는 것을 의미한다. 계의 운동이 평형 위치로부터 작은 변위만을 갖는다면, 우리는 모든 원자들의 변위 x_i가 공통의 각속도 ω 로 다음과 같이 표현된다고 가정할 수 있다. 

이때 A_i 는 원자 i 가 운동을 시작하는 위상을 포함하도록 정의되는 복소수이다. 

일반물리학에서 다루었던 가장 간단한 1차원의 단진자 1 개를 생각해보자. 이 단진자에 대한 뉴튼 방정식은 

이다. 이때 normal mode 의 조건

을 만족하는 해가 존재하는지 알아보자. 운동방정식에 대입하면

이를 만족하는 각진동수가 존재한다면, 이는 곧 normal mode 가 존재함을 뜻한다. A = 0 은 그런 normal mode 가 존재하지 않음을 뜻하므로 흥미로울 것이 없다. 또 이 조건은 항상 성립하여야 하므로 exp(iωt)  또한 양변에서 상쇄된다. 그렇다면,

를 만족하는 각속도의 normal mode 가 존재함을 알 수 있다. 여기서 A , 즉, 단진동의 초기 변위와 위상은 운동의 초기 조건에 의해 결정된다. 고전역학에서 뉴튼 방정식의 해는 위치와 속도의 두 초기 조건을 요구하였던 것을 기억하자. 

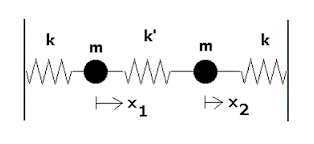
이제 이보다 약간 더 복잡한 일차원의 두 입자로 이루어진 용수철계를 생각해보자. 

입자의 좌표를 각각의 평형위치로부터 x₁ , x₂ 로 정의하자. 뉴튼 방정식은 이제

이 두식을 더하면 (또는 빼면)

를 얻는다. 이 두 입자의 운동은 서로 얽혀있음을 알 수 있다. 이때, q_S = x₁ + x₂ , q_A = x₁ –  x₂ 와 같이 정의하면, 

_{와 같이 정리된다. 이 2 개의 단진동은 서로 얽혀있지 않다. 여기서는 간단하게 2 개만 생각했지만, 실제 상황에 가깝게 아보가드로 숫자 정도의 원자가 존재한다면 서로 얽혀있지 않다는 것이 갖는 위력을 실감할 수 있다. 이때} q_S 모드의 운동은 

과 같다. 또 q_A 모드의 운동은 

과 같다. [참조 : 실제 용수철 계로 같은 상황을 재연한 영상]

여기서 x₁ , x₂ 는 국지적인 좌표이지만 q_A , q_S 는 집합 좌표(collective coordinates)이다. 이 경우에는 간단한 덧셈 뺄셈으로 집합좌표가 구해졌지만, 일반적으로는 계의 대칭성을 사용하여, 즉, 군론(group theory)을 활용하여 이 과정을 수행하게 된다.

위의 예제를 일반적인 방법을 사용하여 풀어보자. 위의 계에 normal mode 가 존재한다면

로 놓았을때 각속도 ω 의 값이 존재하여야 한다. 어차피 좌표는 실수이므로 Re{} 표현은 생략하자. 

이를 정리하면, 

이것이 방정식이라면 해는 X₁ = X₂ = 0 인데, 이는 일반적인 ω 의 값에 대해 normal mode 가 존재하지 않는다는 뜻이 된다. 단, 

을 만족하는 ω 의 값에 대해서는 X₁ = X₂ = 0  이 아닌 해가 존재한다. 이는 전형적인 고유치문제(eigenvalue problem)이다. 

이때 대칭적인 normal mode 의 주파수 

를 대입하면

이 성립하여야 한다. 따라서 X₁ = X₂ = 1  이 된다. 이는 두 원자가 같은 방향과 위상으로 함께 운동하는 모드이다.

비대칭적인 normal mode 의 주파수 

를 대입하면 

이 된다. 따라서 X₁ = – X₂ = 1 이 성립하여야 한다. 이는 두 원자가 서로 반대되는 방향으로(즉, 같은 크기와 π 만큼의 위상차로) 운동하는 normal mode 이다.