에 의해서 온도 T 가 정의된다. 엔트로피 S (즉, 미시 상태의 갯수 Ω)를 U 의 함수로 구하는 것이 최우선적으로 해야 하는 일이다.
인 3N 차원 구의 내부이다. 이 구의 체적은
이 되어 이상기체의 상태 방정식을 얻게 된다.
이때 Ω(U) 를 에너지 U 보다 작은 에너지 상태에 존재하는 미시상태의 갯수로 계산하더라도 문제가 없다. 이것은 매우 많은 입자로 이루어진 계이기 때문에 가능하다. 다음 [예 1]을 보면 이해가 쉬울 것이다.
이때 공간 좌표의 적분 구간은 0 부터 L 까지이고, 운동량 좌표의 적분 구간은 U < E 이다. 공간 좌표 적분을 먼저 하면
[예 1] N 개의 자유 입자가 한변의 길이 L 인 용기 내에 존재할 때, U < E 를 만족하는 미시 상태의 갯수 Ω(E) 를 구하라.
풀이 :
먼저 고전역학적 상태는 모든 입자들의 위치와 속도를 명시한 것임을 상기하자. 이들은 연속적인 변수인데 어떻게 갯수를 셀 수 있을까? 불확정성 원리가 도움이 된다. 한 짝을 이루는 변수 x 와 px 에 대해서 불확정성 원리는 Δx Δpx > h 를 강제한다. 즉, 어떤 두 상태가 이보다 더 가까우면 이 두 상태를 같은 점으로 취급하여야 한다. 즉, x - px 공간에 최소 단위 알갱이가 존재한다고 생각할 수 있다.
이 계의 에너지는
으로 주어진다.
이며, 이때 적분 구간은 반경
이 된다. 엔트로피를 구하기 위해 로그를 취하고 볼츠만 상수를 곱하면,
엔트로피의 미분을 구하면,
이는 엔트로피가 V 와 E 의 함수로 표현된 꼴 S=S(E,V)이다. 체적 V 가 고정된 상태( dV = 0 )를 생각하면,
이 되어,
을 얻는다. 이는 우리가 익히 알고 있는 이상기체의 내부 에너지이다. 또, 계에 열에너지가 유입되거나 방출되지 않으므로( dQ = TdS = 0 ), 위의 식에서 dS = 0 으로 놓으면
이 예로부터 우리는 계의 엔트로피가 열역학적인 성질을 기술하는데 핵심적인 역할을 함을 알 수 있다.









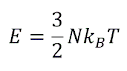

댓글 없음:
댓글 쓰기
내용에 오류가 있거나 질문이 있으면 남겨주세요. (숙제 제외)