14. Helmholtz Free Energy, Gibbs Free Energy, Chemical Potential

1. Helmholtz Free Energy

Helmholtz free energy 𝐹 = 𝐸 − 𝑇𝑆 와 같이 정의되었으며, 이는 우리가 생각하는 계의 변수 𝑆 를 𝑇 로 대치하는 것이었다. 수학적으로 이와 같은 변환을 Legendre transformation 이라고 한다.

𝑑𝐹 = 𝑑𝐸 − 𝑑(𝑇𝑆) = 𝑇𝑑𝑆 − 𝑝𝑑𝑉 − 𝑇𝑑𝑆 − 𝑆𝑑𝑇 = − 𝑆𝑑𝑇 − 𝑝𝑑𝑉

마찬가지로, 계의 변수 𝑉 를 𝑝 로 대치하는 것이 편리한 상황이 있다. 그럴 경우, 엔탈피(enthalpy) 𝐻 = 𝐸 + 𝑝𝑉 를 생각한다. 

𝑑𝐻 = 𝑑𝐸 + 𝑑(𝑝𝑉) = 𝑇𝑑𝑆 − 𝑝𝑑𝑉 + 𝑝𝑑𝑉 + 𝑉𝑑𝑝 = 𝑇𝑑𝑆 + 𝑉𝑑𝑝

거시적 변수 𝑉 가 무엇을 의미하는지 미시적인 관점에서 생각해보자. 기체의 부피는 기체 분자의 부피와 직결되지 않는다. 기체 부피의 대부분은 빈 공간이고, 기체 분자가 차지하는 부분은 매우 작다. 즉, 기체의 부피는 기체 분자의 속성이 아니라, 실린더와 피스톤을 사용하여 기체에 부여된 외부 구속 조건이다.   

어떤 화학 반응을 생각해보자. 실험실에서 대기에 노출된 상태로 두 화학 물질을 반응시켜 다른 화학 물질이 생성될 때, 이 모든 과정은 대기압에서 일어난다. 이와 같은 상황에서 발생되거나 흡수된 열량을 나타내는 것은 엔탈피(enthalpy) 𝐻 = 𝐸 + 𝑝𝑉 의 변화량이다. 반면 폭약 열량 측정 장비의 경우, 밀봉된 상태에서 화학 반응이 진행된다. 이와 같이 계의 부피가 고정되어 있는 경우에 발생되거나 흡수된 열량은 내부 에너지 변화량과 같다. 

많은 경우에 Δ𝐸 와 Δ𝐻 는 크게 차이나지 않는다. 예를 들어, 일산화탄소의 연소 반응의 경우, 

2𝐶𝑂(𝑔) + 𝑂₂ (𝑔)  →   2𝐶𝑂₂ (𝑔),      Δ𝐻=−566.0 𝑘𝐽/𝑚𝑜𝑙,    Δ𝐸=−563.5 𝑘𝐽/𝑚𝑜𝑙 

으로, 적은 차이 밖에 나지 않는다. 이런 경우, 에너지와 엔탈피의 차이점을 굳이 명시하지 않고 혼용하는 경우도 많다.

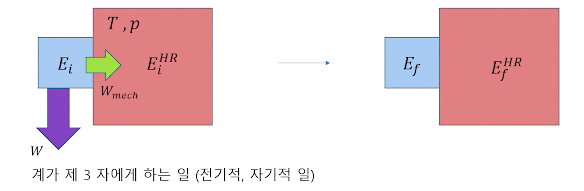
헬름홀츠 자유 에너지는 열저수지와의 열 교환으로 일정 온도가 유지되는 상황에서 계로부터 끌어낼 수 있는 최대한의 가역적인 일과 같다. 단, 열저수지에 역학적 일을 하지 않는다. 

에너지 보존에 의해 Δ𝐸 + Δ𝐸^𝐻𝑅 + 𝑊 = 0 이다. 그런데 열저수지의 부피는 고정되어 있으므로 𝑄^𝐻𝑅 = Δ𝐸^𝐻𝑅 = − (Δ𝐸+𝑊) 이다.  이때 열저수지의 엔트로피 변화량은

이다. 전체의 엔트로피 변화량은

따라서 𝑊 ≤ −Δ𝐹, 즉, 계로부터 끌어낼 수 있는 최대한의 일은 헬름홀츠 자유에너지의 감소량 만큼이다. 또, 계가 일을 하지 않는다면 Δ𝐹 ≤ 0 이다. 즉, 헬름홀츠 자유에너지는 자발적인 과정에서 항상 감소한다.

2. Gibbs Free Energy

이제 깁스 자유 에너지(Gibbs free energy)를 생각하자. 헬름홀츠 자유 에너지를 생각하였을 때, 우리는 엔트로피 𝑆 대신 온도 𝑇 를 독립적인 변수로 택하였다. 또 엔탈피의 경우, 부피 𝑉 대신 압력 𝑝 를 독립적인 변수로 택하였다. 깁스 자유 에너지의 경우, 우리는 온도 𝑇 와 압력 𝑝 를 독립적인 변수로 택한다.

깁스 자유 에너지는 𝐺 = 𝐸 − 𝑇𝑆 + 𝑝𝑉 로 정의된다. 따라서, 𝑑𝐺 = − 𝑆𝑑𝑇 + 𝑉𝑑𝑝 이다. 깁스 자유 에너지는 저수지에 의해 일정 온도와 일정 압력이 유지되는 상황에서 (즉, 부피 변화로 인한 일을 저수지와 주고 받을 수 있다) 계로부터 끌어낼 수 있는 최대한의 가역적인 일 (예를 들어, 전기적, 자기적 일)을 의미한다. 

앞 절에서 헬름홀츠 자유 에너지를 다룬 방법을 다시 적용하면, 𝑊 ≤ −Δ𝐺 , 즉, 계로부터 끌어낼 수 있는 최대한의 비 역학적 일은 깁스 자유 에너지의 감소량 만큼이다. 또, 𝑊 = 0 이라면, Δ𝐺 ≤ 0 이다. 자발적인 과정에서 깁스 자유 에너지는 평형상태에 이를 때까지 항상 감소한다.

3. Chemical Potential

여태 우리는 입자의 개수 𝑁 이 고정되어 있는 상황 만을 생각하였다. 우리가 앞에서 생각했던 microcanonical ensemble 이나 canonical ensemble 에서 𝑁 은 고정되어 있었다. 이제 𝑁 을 변수로 다루어보자. 엔트로피가 𝑁 에 의존하여 변화하는 상황이므로,

𝑆(𝐸,𝑉,𝑁) = 𝑘_𝐵 ln ⁡Ω(𝐸,𝑉,𝑁)

과 같이 쓸 수 있다. 미분을 취하면, 

열역학 제1법칙 ( 𝑁 이 고정된 경우)

와 비교하면, 

,

이다.  이때,

과 같이 화학퍼텐셜(chemical potential) 𝜇 를 정의한다. 이는  𝑑𝐸 = 𝑇𝑑𝑆 − 𝑝𝑑𝑉 + 𝜇𝑑𝑁 과 같이 생각하여도 좋다. 이때 𝜇 는 𝑆 와 𝑉 를 고정시킨 상태에서 계에 입자 1 개를 더하기 위해 요구되는 에너지이다. 즉, 

이다.

Helmholtz free energy 도 입자의 개수를 변수로 포함하도록 정의하면, 𝑑𝐹 = −𝑆𝑑𝑇 − 𝑝𝑑𝑉 + 𝜇𝑑𝑁 

이 된다. 

만일 우리가 입자의 개수보다 전하 𝑄 에 더 관심이 있다면, 𝜇 는 바로 정전기 퍼텐셜과 같아진다.

[연습문제] 화학퍼텐셜을 정의한 두 개의 식, 

  

이 대등함을 증명하여라. 이들은 얼핏 보아 많이 달라 보이지만, 

을 이용하여 쉽게 증명할 수 있다.  (𝑥,  𝑦,  𝑧 대신 𝐸,  𝑁,  𝑆 를 대입하여라.)