이상기체계에서 입자의 퍼텐셜에너지는 무시할 만하다. 간혹 일어나는 다른 입자와의 충돌을 제외하면, 입자들은 다른 입자와의 상호 작용 없이 자유로운 운동을 하기 때문이다. 입자 간의 충돌은 물론 입자 사이의 상호작용에 의한 것이지만, 충돌의 세부 사항은 기체 상태에서 그리 중요하지 않다. 입자들의 충돌로 인한 주된 효과는 기체가 평형상태를 이루는 것인데, 우리는 이미 평형 상태를 가정하고 있기 때문이다.
그러나 고체계의 경우 입자들은 강력한 퍼텐셜에너지에 의해 속박되어 있다. 입자들은 결정 내의 고정된 위치에 배정되며, 제 자리를 중심으로 작은 변위의 운동을 한다. 이때 평형 위치에서 벗어난 변위에 비례해서 복원력을 받는다고 가정하자. 이를 harmonic approximation 이라고 한다. 변위의 3 차항 이상의 고차항이 존재하지만, 이들의 주된 효과는 계가 평형을 이루는데 기여하는 것이므로 무시하기로 한다. 이 또한 우리는 이미 평형 상태를 생각하고 있기 때문이다.
N 개의 입자로 이루어진 고체계는 3N 개의 진동수를 갖는 독립적인 단진자계로 치환된다. 이 각각의 단진자를 normal mode 라고 한다. 이 normal mode 들은 마치 이상기체계의 입자들처럼 주변의 다른 normal mode 들과 상호작용을 거의 하지 않는다. 이때 고체계의 에너지는
이다. 변수를 변환하여 계수를 제거하자.
이제 계의 에너지는
원래의 정의에서 계의 상태 {p, x}가 차지하는 부피가 h3N 이었으므로, 변환 후 {P, Q}가 차지하는 부피는
이 된다. 이제 계의 에너지가 U < E 일 때 가질 수 있는 미시 상태의 개수 Ω(E) 는 6N 차원 초월 공간에서 반지름 E1/2 인 구의 부피를 위의 상수로 나눈 것이므로
이 된다. 엔트로피는




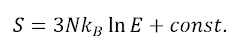

댓글 없음:
댓글 쓰기
내용에 오류가 있거나 질문이 있으면 남겨주세요. (숙제 제외)