양자역학의 도입으로 비로소 흑체복사 문제가 해결되었다. 그러나 아직도 미묘한 문제가 남아 있다. 그것은 깁스 파라독스(Gibbs paradox)이다.
이상기체의 분배함수로부터 엔트로피를 계산하자.헬름홀츠 자유 에너지는
이제 엔트로피는
이 결과를 보면 한 가지 문제가 있다. 통계역학에서 intensive quantity 는 계의 온도, 압력 등의 물리량인데 이들은 같은 균일한 계를 n 배로 증가시켜도 변화하지 않는 물리량들이다. 또, extensive quantity 는 계의 크기를 n 배로 증가시키면 바로 n 에 비례하여 증가하는 물리량인데, 에너지, 엔트로피, 부피 등이다. 위 식의 [ ] 속에는 extensive quantity 가 있어서는 안된다. 따라서 ln 𝑉 항은 문제가 된다.
이 두 계를 분리하는 벽을 없앤다면, 기체 분자들은 온 공간으로 확산할 것이다. 이제 엔트로피는 각각
이때 엔트로피의 변화량은
만일 이 두 이상기체계가 완전히 같은 계라면, 두 계를 분리하는 벽을 없앴다고 엔트로피가 증가하여서는 안된다. 원점으로 돌아가서, canonical ensemble 에서 이상기체의 분배함수 계산을 검토해보자.
이 합을 적분으로 대체할 때, 위상 공간에서의 체적소
𝑑𝑥1 𝑑𝑦1 𝑑𝑧1…𝑑𝑥𝑁 𝑑𝑦𝑁 𝑑𝑧𝑁 𝑑𝑝1𝑥 𝑑𝑝1𝑦 𝑑𝑝1𝑧…𝑑𝑝𝑁𝑥 𝑑𝑝𝑁𝑦 𝑑𝑝𝑁𝑧 내에는
(𝑑𝑥1 𝑑𝑦1 𝑑𝑧1…𝑑𝑥𝑁 𝑑𝑦𝑁 𝑑𝑧𝑁 𝑑𝑝1𝑥 𝑑𝑝1𝑦 𝑑𝑝1𝑧…𝑑𝑝𝑁𝑥 𝑑𝑝𝑁𝑦 𝑑𝑝𝑁𝑧 )/ℎ3𝑁 개의
(구별 가능한) 미시 상태가 존재한다.
이것은 양자역학적인 identical particle (동일 입자)의 개념이 적용되지 않은 형태이다. 즉, 우리는 이 𝑁 개 입자들을 구분(identify)할 수 없다. 어느 입자가 1 번이고 어느 입자가 2 번인지 알 수 없기 때문에, 미시 상태의 개수는 1/𝑁! 배로 줄어들어야 한다. 즉, 𝑁 개의 입자로 만들 수 있는 순열의 개수로 나누어야 한다. 그렇다면 미시상태의 개수는
(𝑑𝑥1 𝑑𝑦1 𝑑𝑧1…𝑑𝑥𝑁 𝑑𝑦𝑁 𝑑𝑧𝑁 𝑑𝑝1𝑥 𝑑𝑝1𝑦 𝑑𝑝1𝑧…𝑑𝑝𝑁𝑥 𝑑𝑝𝑁𝑦 𝑑𝑝𝑁𝑧 )/𝑁!ℎ3𝑁 개가 되어야 한다. 이제
분배함수는
이를 계산하면,
이 된다. 에너지와 압력에는 변화가 없지만, 엔트로피의 값은 달라진다. 헬름홀츠 자유에너지로부터
Stirling 의 공식 ln 𝑁! = 𝑁 ln 𝑁 − 𝑁 을 적용하면,
이는 Sackur-Tetrode equation 으로 알려져 있다. 우변 괄호 속의 표현은 완전히 intensive quantity 로 이루어져 있음을 볼 수 있다. 엔트로피는 괄호의 𝑁 배이므로 extensive quantity 가 된다.
이제 동일한 두 이상기체계의 경우를 생각해보자. 분리된 상태에서 각각의 엔트로피는
뒤섞인 상태에서 전체 엔트로피는
두 기체가 동일한 종류라면, 우리의 예측대로 엔트로피는 증가하지 않음을 알 수 있다.
그러나 두 기체가 구별 가능한 종류라면, 두 기체는 각각 전 공간으로 확산할 것이며, 이들의 엔트로피는 각각
이때 총엔트로피의 변화량은 Δ𝑆𝑡𝑜𝑡𝑎𝑙 = 2𝑁𝑘𝐵 ln 2 가 된다. 이를 entropy of mixing 이라고 한다.
이것은 고전역학적인 통계역학으로는 해결할 수 없는 문제이며, 양자역학 도입 전에 깁스가 발견하였기 때문에 Gibbs paradox라 한다.

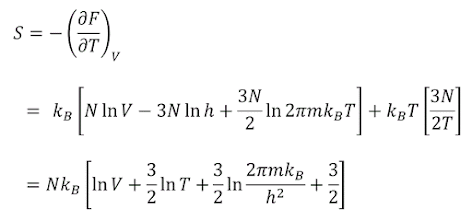













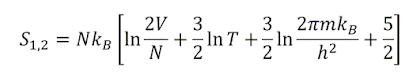
댓글 없음:
댓글 쓰기
내용에 오류가 있거나 질문이 있으면 남겨주세요. (숙제 제외)