앞에서 얻었던 결과를 분석해보자.
이것은 조금 복잡하게 보이지만, 우선 한가지 극한을 생각해보자. 이 극한에서 fugacity 𝔷=𝑒𝑥𝑝(𝛽𝜇) 가 매우 작다고 가정하자. 즉, 𝔷≪1 인 경우를 생각해보자.
를 대입하고 적분을 행하면,
즉,
이는 열파장이 평균 입자 간격보다 훨씬 작아야 한다는 조건과 동일하다. 즉, 이것은 고전역학적인 극한에 해당한다.
얼핏 생각할 때, 𝔷 = 𝑒𝑥𝑝(𝛽𝜇) ≪ 1 이라면 𝛽𝜇 → −∞ 이어야 하는데, 고전역학적 극한에서 𝑇 → ∞, 즉, 𝛽 → 0 이므로 이상하게 느껴질 수 있을 것이다. 그러나 앞에서 언급했던 바와 같이, 입자의 개수 𝑁 이 고정되어 있는 상황에서 𝑇 가 변화하면 𝜇 도 따라 변화한다.
즉, 𝛽 → 0 인 극한에서 𝛽𝜇 → − ∞ 가 유지될 정도로 𝜇 → −∞ 인 것이다. 입자의 개수나 부피가 일정하다면, 위 식에서 𝔷 ~ 𝜆3 ~ 𝑇(−3/2) 가 성립하게 된다.
이제 상태방정식을 계산해보자. 앞에서 boson 자유기체에 대해 𝑝𝑉 = (2/3) 𝐸 임을 보였었다.
다시 𝑥 = 𝛽𝐸, 𝑥 = 𝑢2 로 치환하면
이 식에서 𝔷 를 소거하면 우리에게 익숙한 𝑁 / 𝑉 로 표현된 식을 얻게 된다. 𝔷 ≪ 1 인 경우를 생각하고 있으므로
에서 𝔷 의 1 차항만을 취하여
를 얻게 된다. 이제 앞에서 구한 에너지에 𝔷 를 대입하면
이때 𝑝𝑉 = (2/3) 𝐸 를 이용하면
이 됨을 알 수 있다. 즉, 높은 온도에서 boson 이상기체의 상태방정식은 고전적인 이상기체의 상태방정식에 접근한다. 또한 수정항은 온전히 양자역학적 Bose-Einstein 통계로 인하여 생겨났으며, 압력을 감소시키는 효과를 갖는다.
이제 양자역학적인 효과가 두드러지게 나타나는 저온에서의 특성을 알아보자. 𝜇 < 0 이어야 grand partition function 이 수렴하므로, 0 < 𝔷 < 1 이어야 한다. 높은 온도의 극한이 𝔷→0 이었으므로, 저온 극한은 𝔷→1 이다.
저온 극한 𝔷→1 을 택하여 계의 에너지와 입자 개수를 다시 계산할 수 있다. (이것은 약간 복잡하므로, 대략적인 상황을 설명하는 것으로 대치하려 한다.) 계의 𝑁 / 𝑉 를 고정시킨 상태에서 온도를 낮추어 가면 어떤 임계 온도 𝑇𝑐 에서 𝔷 = 1 에 도달한다고 가정하자. 임계온도를 구하면,
로 주어진다. 이 표현에는 한 가지 문제가 있다. 즉, 온도가 임계 온도보다 낮아지면, 계의 입자 개수가 줄어들어야만 한다. 낮은 온도에서 입자가 사라진다는 것은 비합리적이므로, 이것이 어디에서 연유한 것인지 살펴보아야 한다.
분배함수의 표현에서 합을 적분으로 치환하면서 상태밀도함수
를 도입하였는데, 이 표현에서 𝑔(𝐸 = 0) = 0 이다. 즉, ground state 를 무시하고 적분을 했는데 이것이 임계 온도보다 낮은 온도에서 문제가 된다.
Bose-Einstein 분포에서 평균 입자 개수는
이때 기저상태 𝐸0 = 0 에 존재하는 입자의 평균 개수
은 어떻게 변할까? 일반적인 𝔷 의 경우, 기저상태에 존재하는 입자의 개수는 그리 많지 않기 때문에 문제가 되지 않는다. 그러나 𝔷 가 1 에 매우 근접할 경우, 거시적인 개수의 입자가 기저상태에 존재하게 된다.
이와 같은 현상을 보스-아인슈타인 응축 (Bose-Einstein condensation)이라고 한다. 이때 압력은 온도에 의존하나 입자의 밀도 𝑁 / 𝑉 에는 의존하지 않게 된다. 또 보스-아인슈타인 응축이 일어나는 계의 열용량은 임계 온도 𝑇𝑐 전후에서 뾰족한 봉우리를 갖게 된다.
헬륨은 저온에서 초유체 현상(superfluidity)을 보이는데 이도 보스-아인슈타인 응축의 한 예이다.
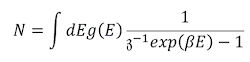
댓글 없음:
댓글 쓰기
내용에 오류가 있거나 질문이 있으면 남겨주세요. (숙제 제외)