엔트로피의 개념은 19 세기 중반 독일 과학자 Clausius 에 의하여 도입되었다.
우리가 흔히 사용하는 내연기관들은 모두 열기관이다. 이들은 실용성을 위하여 열효율을 희생한다. 열효율이 극대화되려면 열기관은 모든 과정이 (거의) 가역적으로 일어나는 카르노 기관(Carnot engine)이 되어야 한다. 카르노 기관은 매 순간 (거의) 열평형을 이루면서 작동하므로, 매우 느리게 작동하는 극단적인 느림보 기관이다.최대의 열효율을 갖는 카르노 기관이 높은 온도 TH 인 열저수지로부터 QH 만큼의 열을 흡수하고, 낮은 온도 TC 인 열저수지로 QC 만큼의 열을 방출할 때,
의 관계가 성립한다. 이 관계식을 카르노 기관이 한 사이클을 마치고 원 상태로 돌아올 때까지 여러 개의 다른 온도를 가진 열저수지와 각각 열에너지를 교환하였다고 생각하면, (흡수한 열량을 + , 방출한 열량을 − 로 정의할 때)
와 같이 표현할 수 있다. 이때 열에너지를 모두 더한 것은
이며, 계가 원 상태로 복귀하였으므로 열역학 제1법칙에 의해 계가 외부에 한 일과 같다. 한편 열에너지나 일과는 달리, 열량 dQ 를 온도 T 로 나눈 함수는 계가 원 상태로 돌아오면 원래의 값으로 돌아오는 것을 알 수 있다. Clausius 는 이를 엔트로피라고 명명하였다.
이 미분 형태를 적분하면 엔트로피 S를 구할 수 있다. 즉, 준정적 과정에서 열량 dQ = T dS 이다. 이를 사용하여 열역학 제1법칙을 표현하면 TdS=dU+pdV 가 된다.여기서 한 가지 첨언하자면, 계가 원래 상태로 돌아온다라는 말에서 유추할 수 있겠지만, 이때의 상태는 미시적인 상태일 수 없고 거시적인 상태, 즉, 압력 p, 부피 V, 온도 T 로 규정되는 상태를 의미하여야 한다. 열역학적 기관이 원래의 미시적인 상태로 돌아가는 것은 불가능하기 때문이다. Clausius 당시는 원자의 존재 여부에 대해서도 의견이 분분하던 시대였으므로, 미시적인 관점은 논의되지도 않았다.

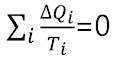

댓글 없음:
댓글 쓰기
내용에 오류가 있거나 질문이 있으면 남겨주세요. (숙제 제외)