보충자료4. 응집물질의 진동(III)

많은 경우에 우리는 탄성파의 세부 정보를 필요로 하지 않는다. 마치 우리가 이상기체를 다룰 때, 이상기체 분자의 위치와 운동량을 필요로 하지 않았던 것과 같다. 우리가 필요한 normal mode 의 정보는 바로 그 진동 주파수 ω들이다. 

각각의 normal mode 는 단진자와 같으므로 우리는 앞에서 다룬 양자역학적 단진자의 결과를 이용하여 계의 진동 에너지를 다음과 같이 표현할 수 있다. 

우리가 다루는 고체계의 원자 수는 아보가드로 숫자 수준이므로, 우리가 계산하여야 하는 normal mode 의 갯수도 그 정도가 된다. 이 합에 명시적으로 나타난 것은 각진동수 뿐이므로 K 에 대한 합을 ω 에 대한 적분으로 바꾸어 계산하는 것이 훨씬 효과적이다. 

각진동수 ω ~ ω + dω 에 속하는 K point 들은 모두 같은 값을 가지므로, 이들의 갯수 dN 을 세어야 한다. 이때 dN 은 dω 에 비례하므로 

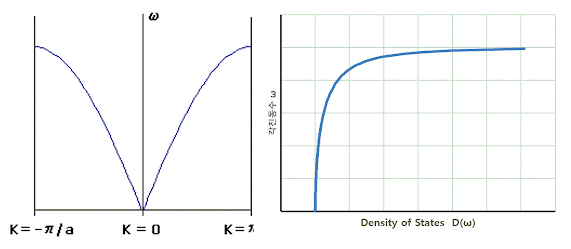
이다. 이때 D(ω) 를 상태 밀도(DOS, Density of States)라고 한다. 그림의 1 차원 탄성계의 경우, K point 들은 균일한 간격 2π/Na 간격으로 존재한다. 즉, 

이다. 따라서, 상태 밀도는

로 주어진다. 우리의 1차원 탄성계에서 이것은 

이때, 분모가 0 이 되는 각진동수에서 상태 밀도가 발산하지만 이것은 실제로 걱정할 필요가 없다. 상태의 숫자 자체는 잘 정의된 숫자이기 때문에 적분을 행하면(즉, 상태 밀도에 각진동수 영역을 곱하면) 이는 잘 정의된 결과를 내어놓을 수 밖에 없기 때문이다.

 

이제 고체계의 진동 에너지는

로 표현된다. 이를 온도 T 로 미분하면 비열을 계산할 수 있으며, 이는 바로 실험 결과와 비교 가능하다. 1912 년에 Debye 는 원자의 열 진동이 고체의 비열에 기여하는 부분을 설명하는 이론을 발표하였다. 이 시절에는 아직 원자 간의 상호 작용을 정확하게 기술할 능력이 없어서 상태 밀도 함수를 알 수 없었지만, Debye 는 분산 관계식의 원점 부근에서의 기울기가 음파의 속도라는 사실을 활용하였다. 

실험에서 측정된 고체 내의 음파 속도를 활용하여 Debye 는 저온에서 고체의 비열이 T³ 에 비례함을 설명하였다. 

아인슈타인도 1907 년에 고체의 비열을 설명하려고 시도하였었다. 그는 고체를 이루는 모든 단진자가 같은 각진동수로 진동한다고 근사하였다. 이는 optic branch 에 적용하기에는 적절하였으나 acoustic branch 에는 적절하지 않다. 따라서 고온에서의 비열은 잘 예측하였지만, 저온에서는 정성적으로 틀린 예측을 하게 된다. 이에 반해, Debye 의 모델은 저온에서 비열이 T³ 에 비례하는 것을 정확하게 예측하였다. 

[Peter Debye, By Unknown author - http://chem.ch.huji.ac.il/~eugeniik/history/debye.html, Public Domain, https://commons.wikimedia.org/w/index.php?curid=1083819]