이제 fermion 들로 이루어진 기체, Fermi gas 를 다루어보자. 이들은 파울리 배타 원리에 의해 한 양자역학 상태에 입자 하나 밖에 들어가지 못하는 성질을 가졌다. 금속 내부에 존재하는 전자들을 Fermi 기체로 취급함으로써 많은 것을 설명할 수 있다. 전자 사이의 쿨롱 힘이 존재하는 상황에서 이것은 의외로 느껴지겠지만, 주변에 얼마나 많은 전자들이 존재하는 상황인지를 고려하기만 한다면, 그 상황에서의 "평균적인 전자"들은 마치 기체 입자들처럼 상호작용이 거의 없는 것처럼 다룰 수 있다.
기체 상태에서는 입자 간의 상호작용을 무시하더라도 계의 성질이 잘 기술될 수 있다. 예를 들어, 고전역학적으로 기술한 기체의 경우, 기체 분자들의 상호 작용은 단지 기체 분자들 간의 에너지 재분배를 확보하는 역할을 하기 때문에, 계가 평형 상태에 도달했다는 가정 속에 자동적으로 포함된다.
기체 분자들은 평균적으로 서로 멀리 떨어져 있기 때문에 서로에게 끼치는 영향이 미미한 것은 이해하기 쉽다. 그러나, 전자처럼 원거리에서도 작용하는 정전기력으로 먼 곳에 있는 다른 전자와 상호작용을 할 수 있는 경우는 기체처럼 취급할 수 없을 것 같아 보인다. 그러나, 의외로 강력한 상호작용을 하고 있는 입자들의 "평균적"인 운동도 기체 상태 입자의 운동처럼 유유하게 보일 수 있다.
위 사진은 물고기 무리의 모습이다. 물고기들은 상대와 충돌하는 일 없이 거리를 유지한다. 이는 서로 강하게 작용하는 입자계를 닮았다. 동시에 이들은 마구 부닥치는 혼돈 상태에 빠지지 않고 유유히 헤엄친다. 마치 다른 물고기가 자신들의 진로를 방해하는 적이 없는 듯하게 느껴진다.
단순한 물고기만 생각하지 말고, 물고기와 그 주변의 평균적인 환경을 더한 것을 "평균적 물고기"라고 생각해보자. 이런 "평균적 물고기"는 다른 "평균적 물고기"와 충돌하지 않고 마치 자유로운 입자인 것처럼 행동할 것이다. 마찬가지로, 강하게 상호작용하는 전자들도 주변의 평균적인 환경(screening)을 더한 것을 "평균적 전자"라고 생각한다면, 이들은 서로 상호작용하지 않는 자유 입자인 것처럼 행동할 것이다.
여러분은 양자역학에서 무한 퍼텐셜 문제를 푼 적이 있을 것이다. 일련의 고유치와 고유함수를 구한 다음, 난데없이 이 퍼텐셜에 전자 5 개가 존재한다면 어떤 에너지 준위에 있게 되겠는가라는 질문을 접하였을 것이다. 아마도 여러분은 기저 상태로부터 스핀을 고려하여 한 에너지 준위에 2 개의 전자가 최대한으로 존재할 수 있다고 가정하여 답하였을 것이다. 이러한 답을 제출하면서도 마음 한 편으로는 전자-전자 간의 강한 상호 작용을 어떻게 무시할 수 있는 것인지 의문을 가졌다면, 그것은 매우 온당한 질문을 던진 것이다.
이제 우리가 어떤 수단으로 이런 까다로운 문제를 접근하는지 힌트를 얻었을 것이다. 우리가 이러한 다체문제(many-body problem)을 다루는 기본 방식은 그들을 모두 "평균적"인 존재로 만드는 것이다. 무한 퍼텐셜 하에 놓인 것은 "평균적인 전자"인 것이다. 이것이 밀도 범함수 이론(density functional theory)의 초간단 요약이다.
서로 상호작용하지 않는 fermion 으로 기술 가능한 계의 예로는 금속 내의 전자, 액체 헬륨-3, 백색 왜성, 중성자 별 등을 들 수 있다. fermion 들은 계에 속하는 임의의 두 입자를 교환할 때, 계의 파동함수가 원래 값의 -1 배로 되는 성질을 가진 입자들이다. 이들은 반정수(half-integer), 즉, 1/2, 3/2, 5/2, … 등의 스핀(spin)을 갖는다. 이러한 계는 𝜓(𝑟1 , 𝑟2) = − 𝜓 (𝑟2 , 𝑟1) 을 만족한다. 만일 동일한 2 개의 입자(identical particle)가 같은 위치에 존재한다면, 이를 만족하는 파동함수의 값은 0 외에는 없다. 이것이 파울리 배타 원리이다.
fermion 계에 대해 다시 grand canonical ensemble 을 적용하여보자. 어떤 양자 상태에 존재할 수 있는 fermion 의 개수는 0 아니면 1 뿐이다. 따라서, 양자 상태 하나에 대한 분배함수는
모든 양자 상태에 대한 분배함수는 이들의 곱이므로,
이다. 이로부터 계의 입자 수를 계산하면,
boson 의 경우와 달라진 점은 분모에서 – 1 이 + 1 으로 바뀐 것이다. 그리고, fermion 의 경우에는 양자 상태에 존재할 수 있는 입자의 개수가 0 또는 1 이기 때문에 우리는 직접 그 합을 구했으므로, 무한 등비 수열의 수렴 조건을 요구하지 않아도 된다는 점이다. 즉, 이제 𝜇 는 양이나 음의 어떤 값도 취할 수 있게 된다.
fermion 의 스핀 𝑠 에 따라 2𝑠+1 개의 상태를 가질 수 있다. 이를 스핀 축퇴 인자(spin degeneracy factor) 𝑔𝑠 = 2𝑠 + 1 으로 표시하기로 하자. 이때, 서로 상호작용하지 않는 비상대론적 입자 에너지 E=(ℏ2 𝑘2)/2𝑚 를 갖는 fermion 들의 상태밀도함수를 계산해보자.
이 경우 상태밀도함수는 이전에서 구한 상태밀도함수에 스핀축퇴인자를 곱한 것이다.
boson 의 경우에서 행했던 방식대로 진행하면,
Fermi 기체의 압력은 고전적인 이상기체의 압력보다 큰 것을 알 수 있다. 이는 파울리 배타 원리에서 곧바로 추측할 수 있는 현상이기도 하다.
온도 𝑇 → 0 인 극한을 생각하자.

입자들은 가장 낮은 에너지 상태부터 차곡차곡 채워나간다. 마지막으로 채워진 상태의 에너지, 즉, 입자가 갖는 가장 높은 에너지를 Fermi energy 𝐸𝐹 라 한다. 이것은 입자 개수 𝑁 을 고정시킨 상황에서 𝑇 = 0 일 경우의 화학퍼텐셜과 같다.
입자들의 파동함수는 평면파처럼 균일한 크기로 전 공간에 퍼져있게 되며, 운동량 𝑝 = ℏ𝑘 고유치를 갖는다. Fermi energy 𝐸𝐹 에 대응하는 파수(wave number) 를 Fermi wave number 𝑘𝐹, 그때의 운동량을 Fermi 운동량 𝑝𝐹 라 한다. | 𝑘 | < 𝑘𝐹 인 모든 상태들은 입자로 채워지며, 이를 Fermi sea 또는 Fermi sphere 라고 한다. Fermi sea 의 표면을 Fermi surface 라고 한다.
Fermi energy 를 계산해보자.
Fermi energy 로부터 Fermi 온도 𝑇𝐹 = 𝐸𝐹 / 𝑘𝐵 를 정의할 수 있다. 우리가 높은 온도와 낮은 온도를 언급할 때, 그 기준이 되어줄 수 있는 것이 Fermi 온도이다. 일반적으로 Fermi 온도는 상당히 높다. 금속 내 전자의 경우 𝑇𝐹 ~ 104 𝐾 이며, 백색왜성 내의 전자의 경우 𝑇𝐹 ~ 107 𝐾 이다.
계의 평균 에너지와 압력은
이 되어,
이 된다. 이를 축퇴 압력(degeneracy pressure)라 한다. 이는 파울리 배타 원리의 직접적인 결과이며 백색왜성이나 중성자별에서 중요한 역할을 한다. 고전적인 이상기체나 boson 이상기체의 경우와는 극적으로 대비되는 결과이다.


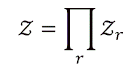







댓글 없음:
댓글 쓰기
내용에 오류가 있거나 질문이 있으면 남겨주세요. (숙제 제외)